Impact of positional uncertainty on species distribution modelling
(Part I)
Species distribution models (SDMs) are used to infer the ecological requirements of species as well as to predict their geographic distribution. Many SDMs have been developed using presence/absence or presence-only species occurrence data. The great majority of these data, especially in the form of presence-only data from museum or herbarium collections or from volunteer observation networks, are available increasingly over the Internet.
Problem of positional uncertainty
One of the problems with the species occurrence data is the uncertainty about where the occurrence was located (positional uncertainty).
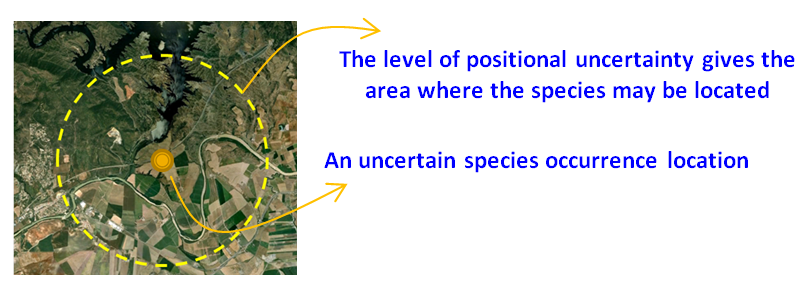
The following figure represents a simulation of positional uncertainty in a location. Positional uncertainty in a point location (e.g. species occurrence) leads to a shift in the point’s position in the x- and y-directions. To simulate the positional uncertainty, a probabilistic approach was used to introduce a positional error (ɛ) with no directional bias in species occurrence. Taking ɛ ~ N(0, distance) gives a normally distributed unbiased error with a standard deviation of the specified distance.

This problem becomes important when the data are used to develop a SDM. Coordinates are used to extract the co-located environmental variables and thus, positional error will transfer to inaccurate characterizations of the species-environment relationship.
Spatial autocorrelation & positional uncertainty
Naimi et al. (2011 and 2012) showed that the impact of this positional uncertainty on performance of species occurrence can be understood by examining spatial autocorrelation in predictors.
This article aims to address the technical aspects of assessing the impact of positional uncertainty in species occurrences on SDMs by examining the spatial autocorrelation in predictors (Part I is based on the first paper, i.e. Naimi et al., 2011, and the Part II is based on the second paper, i.e. Naimi et al., 2012).
First Article (Naimi et al., 2011):
In this study a comprehensive set of analyses were conducted to explore whether the impact of positional uncertainty in species occurrence locations can be linked to spatial autocorrelation in predictors.
Spatial autocorrelation is a statistical property of most ecological variables and represents the relationship between values of the given variable at different geographical separations. It is hypothesized that, in species distribution modelling, errors in species location will matter less if nearby locations have similar environmental characteristics to the true location. Therefore, the robustness of a SDM to species positional uncertainty is expected to be affected positively by spatial autocorrelation in environmental variables.
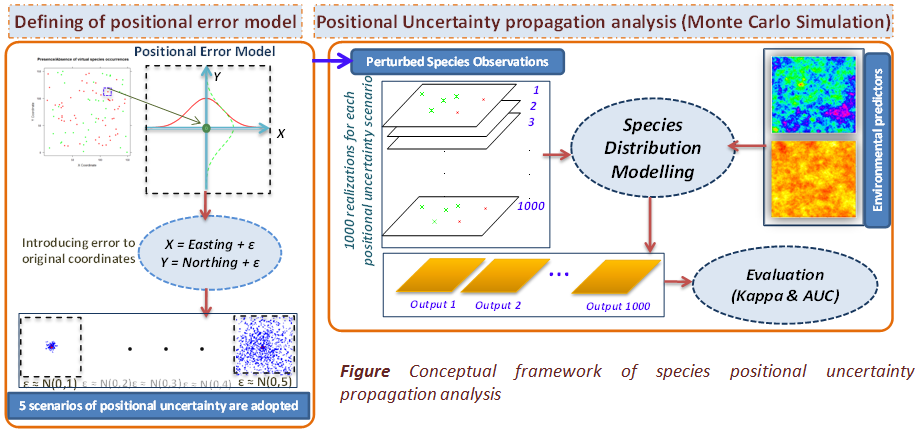
Method: In this study, a series of artificial datasets covering 155 scenarios including different combinations of five positional uncertainty scenarios and 31 spatial autocorrelation scenarios were simulated. The level of positional uncertainty was defined by the standard deviation of a normally distributed zero-mean random variable. Each dataset included two environmental gradients (predictor variables) and one set of species occurrence sample points (response variable).
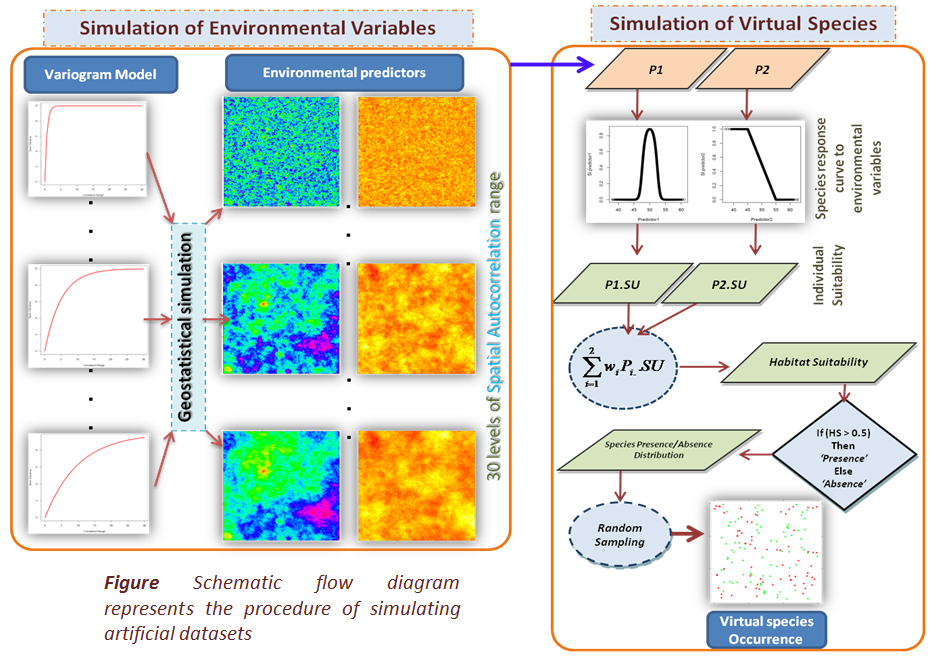
Seven commonly used models were selected to develop SDMs: GLM, GAM, BRT, MARS, RF, GARP and Maxent.
A probabilistic approach was employed to model and simulate five levels of error in the species locations. To analyse the propagation of positional uncertainty, Monte Carlo simulation was applied to each scenario for each SDM. The models were evaluated for performance using simulated independent test data with Cohen’s Kappa and the area under the receiver operating characteristic curve.
Results:
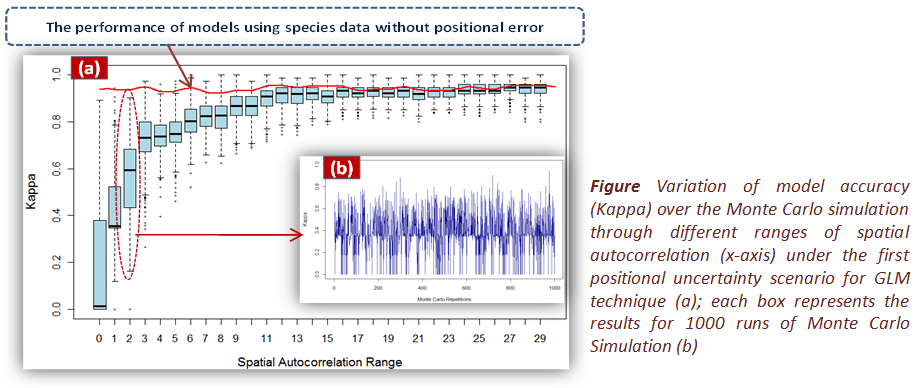
Positional uncertainty in species location led to a reduction in prediction accuracy for all SDMs, although the magnitude of the reduction varied between SDMs. In all cases the magnitude of this impact varied according to the degree of spatial autocorrelation in predictors and the levels of positional uncertainty. It was shown that when the range of spatial autocorrelation in the predictors was less than or equal to three times the standard deviation of the positional error, the models were less affected by error and, consequently, had smaller decreases in prediction accuracy. When the range of spatial autocorrelation in predictors was larger than three times the standard deviation of positional error, the prediction accuracy was low for all scenarios.
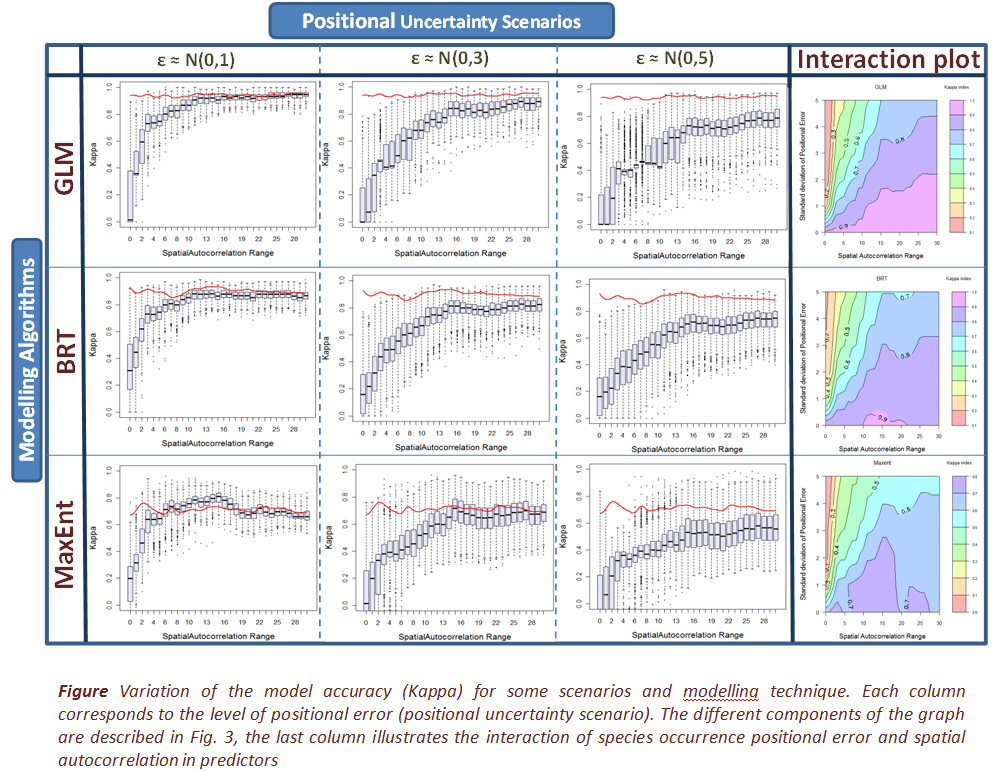
Main conclusion:
It is concluded that examining the spatial autocorrelation in predictors to find the effective autocorrelation range can give insight into whether predictions are likely to be affected by the uncertainty in the sample locations.
Here I show how the spatial autcorrelation in predictors can be examined in predictors (using R), and then how it should be interpreted with respect to the results of the paper.
To understand whether the level of positional uncertainty in species occurrence (I assume that you have an estimation for it) is goint to impact the output, you can compute an empirical variogram for each predictor variable (that has significant contribution to the model), and then interpret the range of sparial autocorrelation.
There are several packages in R, that can be used for computing empirical variogram (e.g. gstat, geoR), but none of them are designed to compute the variogram for a raster dataset. Since the predictor variables in a species distribution modelling effort are usually in a raster format, it would be more appropriate to have a function for computing variogram for a raster dataset (although there are ways to convert raster data to formats using which the implemented functions in the mentioned packages can give the variogram!)
For this purpose, I recommend to use the Variogram function, implemented in usdm package (which I have recently developed) in R to examine the empirical variogram for a raster dataset.
# This example shows you, first, how a raster dataset can be read into R,
# and then, how an empirical variogram can be computed for the raster
library(usdm) # load library of usdm (if it has not been installed, use 'install.packages' function to install it)
# suppose you have the predictor variables as ASCII grid format, so put the file(s) in your working directory
# or for this example, you can download a Dem layer in ascii grid format from here (right-click, select save as, and asve the file into your wiorking directory)
# or you can use your own raster file!
require(rgdal)
r <- raster('Dem.asc')
r
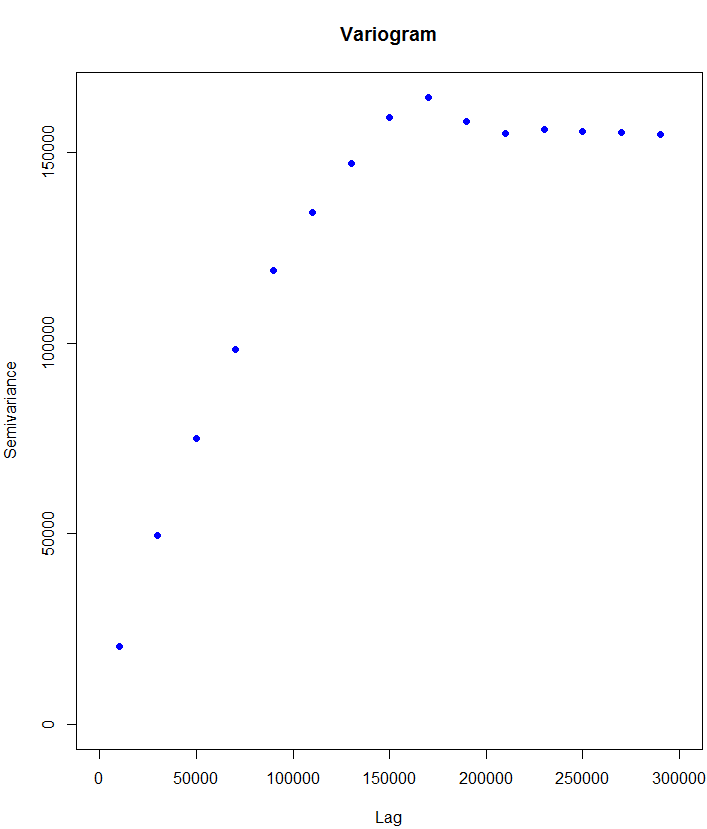
v <- Variogram(r)
plot(v)
# or you can set the parameters of lag, and cutoff (see help of the function!)
v <- Variogram(r,lag=20000,cutoff=300000)
plot(v)
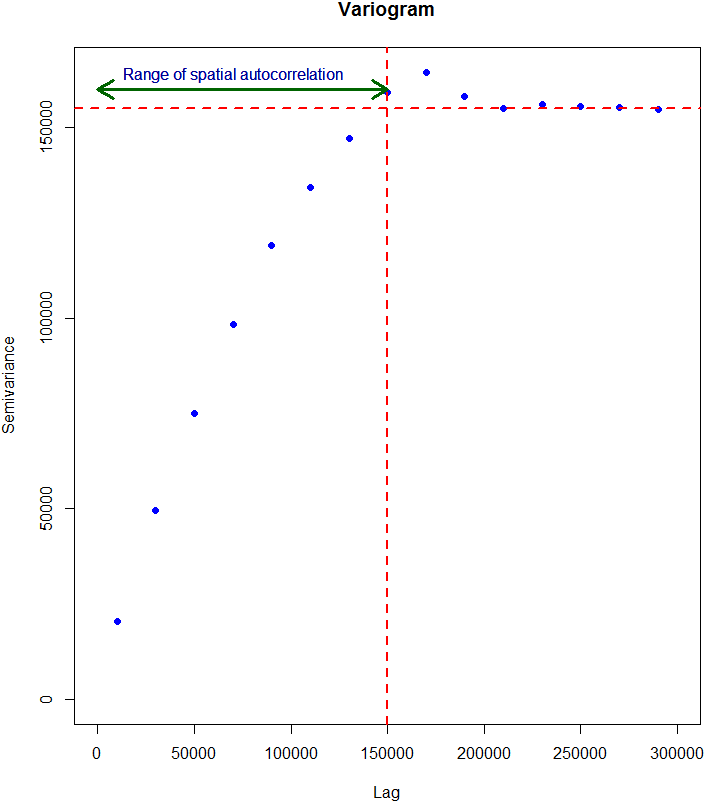
From the variogram, you can interpret the range of spatial autocorrelation, in this case it is 150 km:
So, if you have an estimation of positional uncertainty in your species occurrence data, you can use the interaction graphs for different modelling techniques in the paper (Figure 8 in the paper or Figure S4 in suplementary materials) to interpret how decline in the accuracy of the model is likely as a result of the positional uncertainty. For example, if the level of uncertanity is 50 km, you should consider 1/3 of this value (i.e. 17 km) as standard deviation of the error (assuming that the error has a normal distribution). If you used a Maxent model, following graph (for AUC values) should be used.
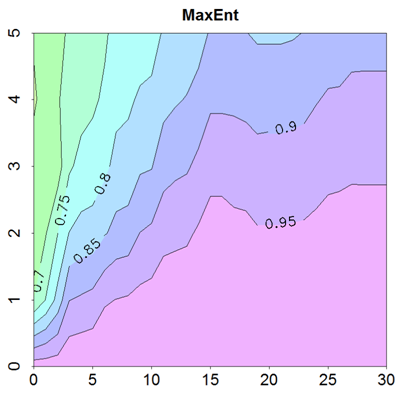
In the graph, the y-axis is the standard deviation of the positional error, and the x-axis is the range of spatial autocorrelation in the predictor. So, for our example, since the standard deviation of the positional error is 17 km, and the range of spatial autocorrelation is 150 km, you should draw a line from 15 on the x-axis, and intersect this line to a line from 1.7 on the y-axis. The level of decline can be interpreted from the contours. It means that the difference between the accuracy measure at the intersection point and the measure for the same range (i.e. 15) but with no positional error (i.e. 0 on y-axix) can be interpreted as the level of decline in the performance. So, in this example you see that the magnitude of the decline in the performance of the maxent model is not important, it means that because of existing spatial autocorrelation in the predictors (you should also check the autocorrelation in the other important predictors), the SDM's prediction has not been affected by the positional uncertainty.
Reference:
- Naimi, B. Skidmore, A.K., Groen, T.A., Hamm, N.A.S. (2011) Spatial Autocorrelation in Predictors Reduces the Impact of Positional Uncertainty in Occurrence Data on Species Distribution Modelling. — Journal of biogeography. 38: 1497-1509

